丨捷克

Michal Bednář | Liquid Blocks

Liquid Blocks

V projektu Liquid Blocks hledám využítí minimálních ploch, které na sebe periodicky navazují ve třech směrech (Triply Periodic Minimal Surface, dále jen TPMS). Snažím se využít specifického způsobu jakým tyto plochy utváří kontinuální, “tekutý“ prostor a obohatit o něj městské prostředí. Díky tomu je možné plynule vystoupat „domem“ až na samotný vrchol, aniž by člověk vstoupil do jeho útrob. Střešní krajina se tak stává volně přístupnou a využitelnou jako plnohodnotný městský prostor.

Samotný projekt je situován do města Plzně. Řešené území se rozpíná od hlavního nádraží k Denisovu nábřeží. V současném stavu toto roztříštěné a pomalu odumírající území neodpovídá své atraktivní poloze v centru města. Cílem projektu je vytvořit plynule průchozí, živou městkou strukturu a dodat tak území novou energii a využití.

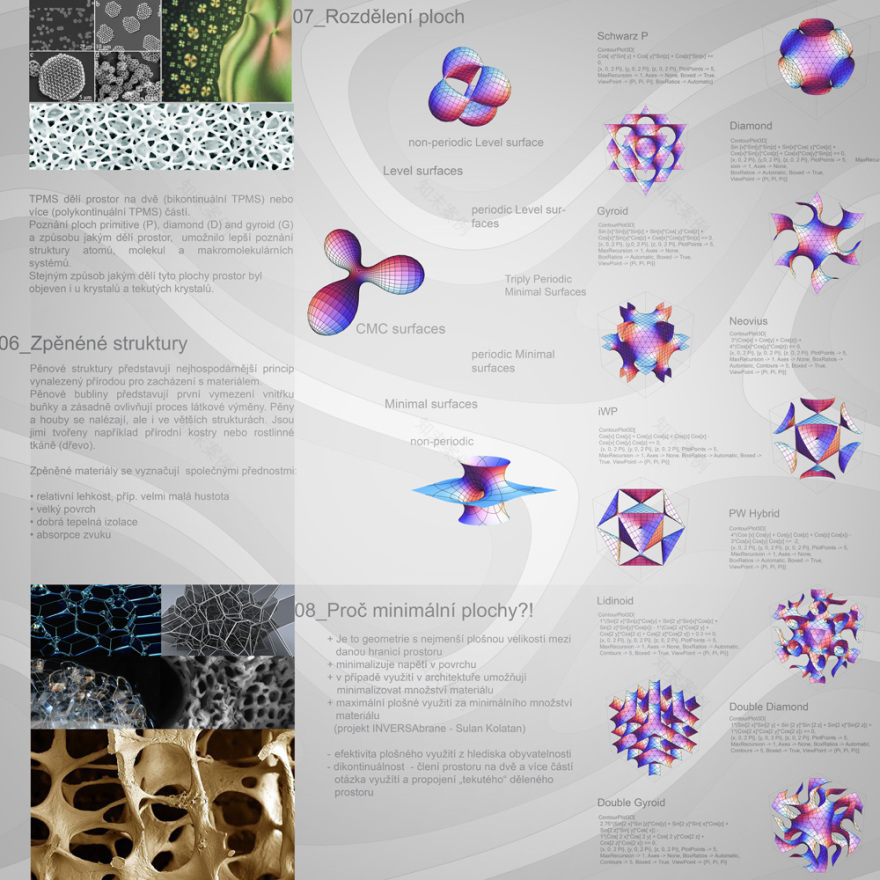
Minimální plochy

Minimální plochy jsou v architektuře využívány již delší dobu a to hlavně v podobě zavěšených lanových anebo membránových konstrukcí. Jednou z nejznámějších a nejrozsáhlejších stavbou v tomto duchu je Olympijský stadion v Mnichově (1972, autoři: Günter Behnisch, Frei Otto). Minimální plochy se však vyznačují zajimavými vlastnostmi, které otevírají nové, a stále dostatečně neprobádané, možnosti jejich dalšího využití.

Minimální plocha zaujímá v daných hraničních podmínkách vždy plochu s nejmenším možným povrchem. To je dobře demonstrovatelné pomocí pokusu s drátěnou smyčkou namočenou do mýdlové vody. Drátěnou smyčku překlene vždy stejná plocha. Toto chování je dáno povrchovým napětím mýdlového filmu, které způsobuje minimalizaci povrchu. Nejjednoduším příkladem minimální plochy je rovinna. Dále to pak může být catenoid (hyperbolický paroboloid) nebo helicoid (šroubovice).

Z hlediska diferenciální geometrie jsou minimální plochy definované nulovou hodnotou středního zakřivení. Střední křivost je vlastnost, která lokálně (ve vztahu k nejbližším bodům na ploše) popisuje zakřivení plochy. Hodnota středního zakřivení vychází z hlavních poloměrů křivosti plochy.

Od 80.tých let, kdy byly matematicky popsány nové druhy minimálních ploch se toto téma dostalo do popředí zájmu matematických a vědeckých studií. A to hlavně z důvodu jejich návaznosti na problematiku nanotechnologií a molekulárního inženýrství. Právě objevení ploch periodicky vyplňujících prostor (TPMS) a způsobu jakým dělí prostor, umožnilo lepší poznání struktury atomů, molekul a makromolekulárních systémů.

Minimální plochy přínáší nový způsob vnímání a utváření prostoru (projekt Hybrid Species). TPMS mají podobné vlastnosti jako zpěněné struktury, které představují nejhospodárnější princip vynalezený přírodou pro zacházení s materiálem. Geometrie těchto ploch umožňuje maximální plošné využití za minimalizace množství materiálu (projekt INVERSAbrane, Kol/Mac studio). Všechny tyto vlastnosti naznačují, že si tato problematika zaslouží svoji pozornost i v architektuře.